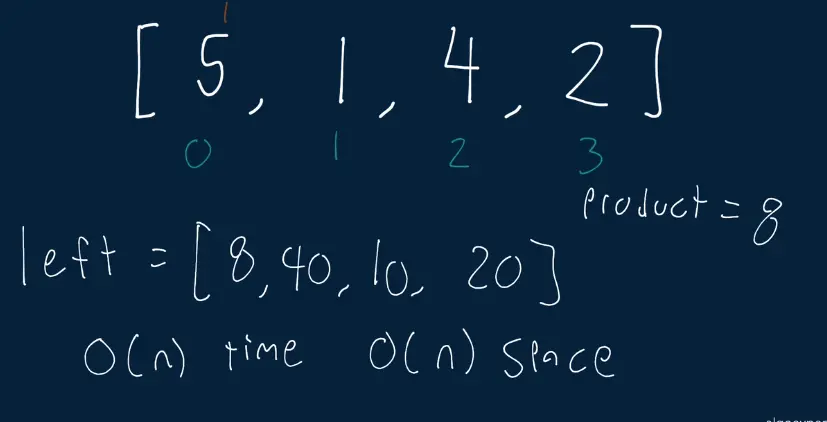Array of products

Date: 2024-07-30

Problem

• We are given an non empty array of integers as input and we have to return an array of the same length, where each element in the output array is equal to the product of every other number in the input array
• For instance, the value at output[i] is equal to the product of every number in the input array other than input[i].

Example

# Sample Input
array = [5, 1, 4, 2]
 
# Sample Output
[8,40,10,20]
# 8 is equal to 1 x 4 x 2
# 40 is equal to 5 x 4 x 2
# 10 is equal to 5 x 1 x 2
# 20 is euqal to 5 x 1 x 4

Solution

Brute Force Solution

• This solution is non optimal and requires two for loops

for i in n:
	for j in n:

• The i will keep track of the current index and j will be the inner loop where we would multiply the values to find the product
• Product is set to 1 for each iteration this way whatever value is first is just carried over.
• Once we’ve iterated over all values that are not equal to i, starting from the beginning then we just append the product to the new array
• This solution gives us an $O(n^2)$ time complexity since we are looping through the array for each single iteration.

Optimal Solution

• A less time costly approach is to iterate through the array and for each individual iteration you can multiply the values to the left and to the right of the current index. Then you got the product and append it to the final array
• Once you find the product for the current index you simply move on to the next index

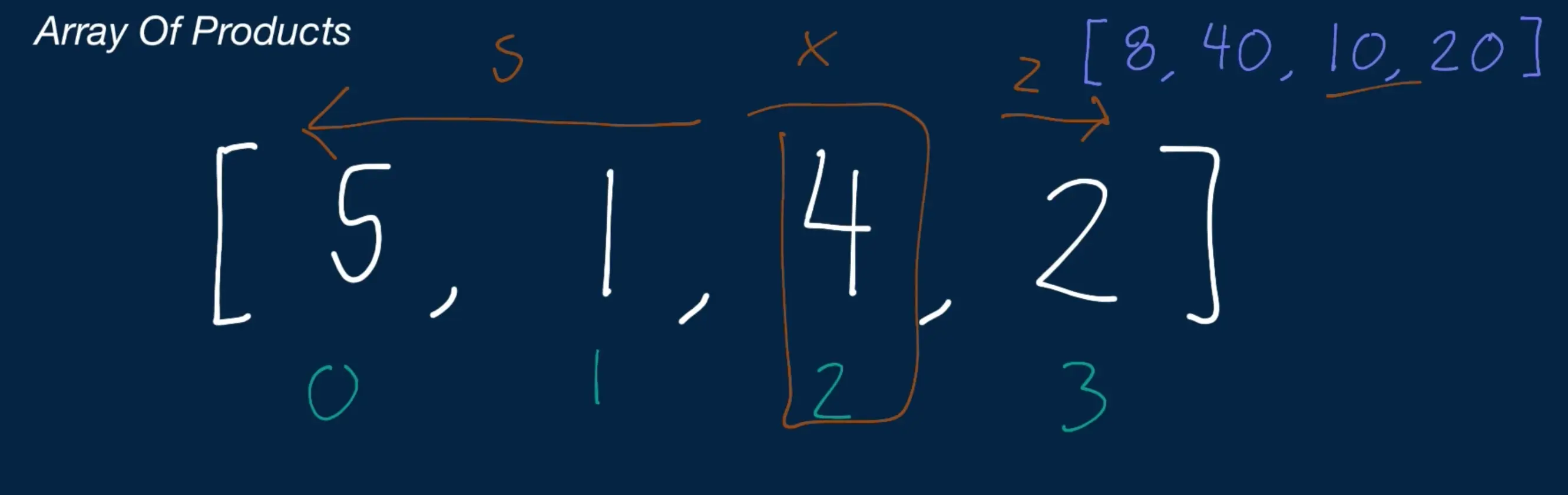
• In code this would be done differently but still the same process.
• We will be defining a left and right array that will each keep track of the current product to the left of index i in the array. For instance, in the array above the first product would be 1 since there’s nothing to the left of the first product. Then the second element or index 1 would be the product of 5 since there is nothing left to the 5. Then moving on to index 2 we have 5 * 1 = 5 and finally our last index we have 5 * 1 * 4 = 20. Therefore now we have the final left array of 1, 5, 5, 20. Then for the right array we have 8, 8, 2, 1. Once we multiply these together we get the final array we wanted 8, 40, 10, 20.
• Time Complexity: $O(n)$ | Space Complexity: $O(n)$

Optimal Solution (less steps)

• Like the previous solution there’s a way to make get to this same solution with less steps in the code. This won’t improve the space or time complexity but would be using less code.
• In this solution instead of creating a right array, after we’ve created the left array and obtained the products to the left of the index we can simply find the products to the right of index in array and start multiplying to the left array as we obtain the products. This prevents us from creating another array and then multiplying it at the end and storing it another array.