Find Kth Largest Value in BST

Date: 09-17-24

---

Problem

• For this problem we’re given a root node of our BST and a second input that is going to be a positive non-zero integer k. Our solution should find the kth largest value in the BST. Meaning if we get the value 3 as k , then we would be trying to find the third largest value in the BST.
• Reminder: A BST node is said to be valid if and only if it is strictly greater than its left child and greater than or equal to its right child.

Note
----
Inorder => Left, Root, Right.
 
Preorder => Root, Left, Right.
 
Post order => Left, Right, Root.

Example:

Sample Input:
tree =   15
       /     \
      5      20
    /   \   /   \
   2     5 17   22
 /   \         
1     3       
k = 3
 
Sample Output: 
17

---

Approach 1 (In-order traversal):

• This approach uses in-order traversal to find the kth largest value. The idea is to traverse the BST in an in-order manner, which is not the most optimal, but would result in obtaining the BST values in sorted order and simply finding the kth value.

Implementation

# This is an input class. Do not edit.
class BST:
    def __init__(self, value, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right
 
 
# O(n) time | O(n) space
def findKthLargestValueInBst(tree, k):
    # Array to hold in order nodes
    sortedNodeValues = []
 
    # Recursive call
    inOrderTraverse(tree, sortedNodeValues)
 
    # Return element from the array
    return sortedNodeValues[len(sortedNodeValues) - k]
 
 
def inOrderTraverse(node, sortedNodeValues):
    if node == None:
        return
 
    inOrderTraverse(node.left, sortedNodeValues)
    sortedNodeValues.append(node.value)
    inOrderTraverse(node.right, sortedNodeValues)    

Complexity Analysis

• Time Complexity: $O(n)$ — we are visiting every node in our BST
• Space Complexity: $O(n)$ — the recursive call stack is of length n and the array we created

---

Approach 2 (reverse in-order traversal):

• Instead of visiting the nodes in order from smallest to larges like the last solution, it would be more efficient to visit the largest nodes in the BST first. To do this we switch the order of operations from left, visit, right to right, visit, left. Also, instead of saving all our nodes in an array, we can simply stop iterating at our kth value.

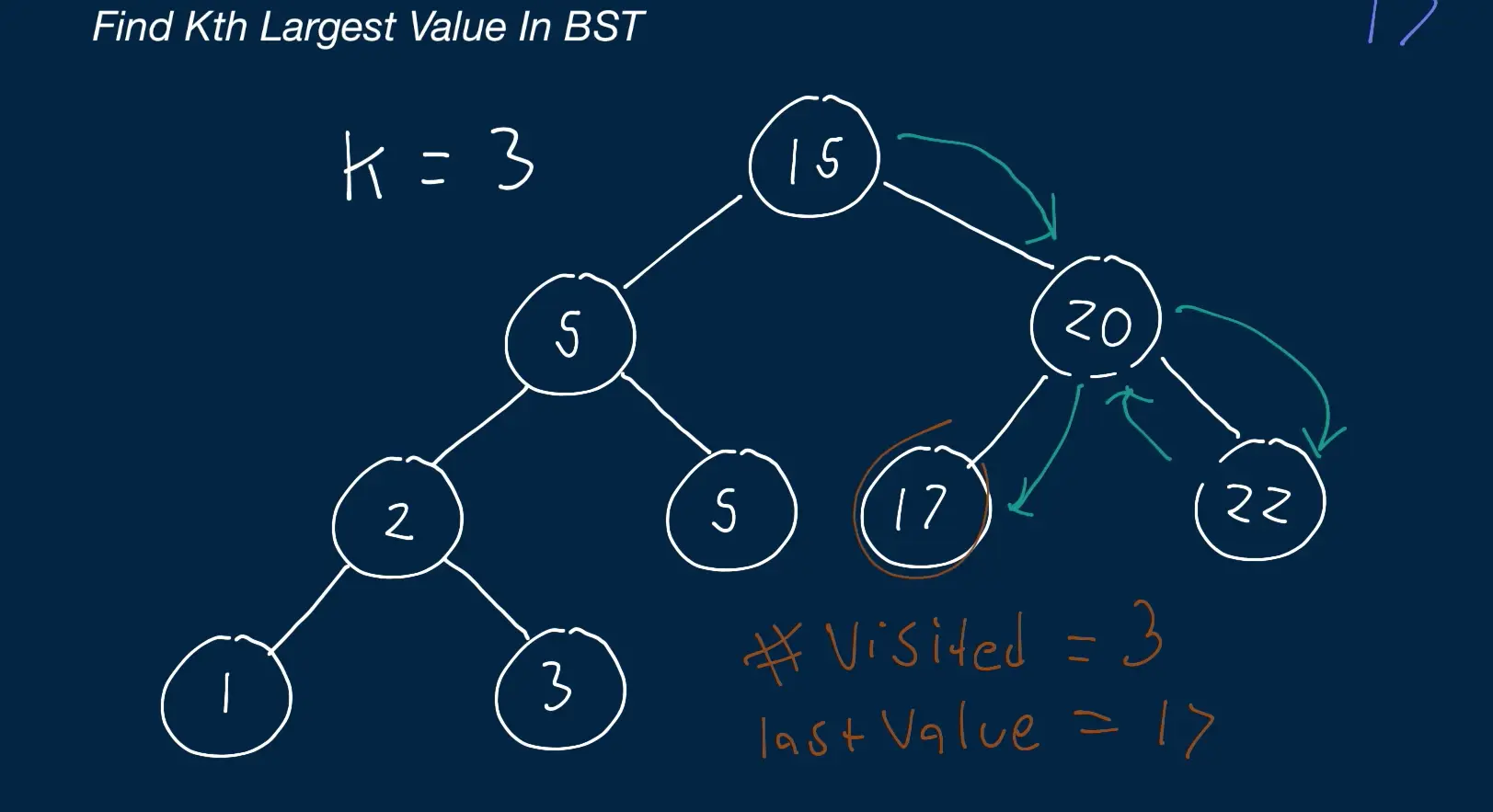
• The only thing we’re storing or keeping track of is the number of nodes visited and the last value. This is unlike our last solution which stored the entire array of nodes.

Implementation

# This is an input class. Do not edit.
class BST:
    def __init__(self, value, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right
 
class TreeInfo:
    def __init__(self, numberOfNodesVisited, latestVisitedNodeValue):
        # The number of nodes we've visited and the value of the last node visited
        self.numberOfNodesVisited = numberOfNodesVisited
        self.latestVisitedNodeValue = latestVisitedNodeValue
 
def findKthLargestValueInBst(tree, k):
    # Create an instance of TreeInfo class
    # 0 to state that we haven't visited any node, and -1 as a placeholder value
    treeInfo = TreeInfo(0, -1)
 
 
    # Reverse Inorder Traversal
    reverseInOrderTraverse(tree, k, treeInfo)
 
    return treeInfo.latestVisitedNodeValue
 
def reverseInOrderTraverse(node, k, treeInfo):
    # if our traversal ends in a empty node or we've visited the kth node then
    # we can stop our recursion
    if node == None or treeInfo.numberOfNodesVisited >= k:
        return
 
    # Otherwise, begin traversing from largest to smallest
    reverseInOrderTraverse(node.right, k, treeInfo)
 
    # If we still havent visited the kth node, then we can update 
    if treeInfo.numberOfNodesVisited < k:
        # Once we've reached the kth node this value gets update the and if statement is not true anymore
        # and we jump out of the recursion using the first if statement
        treeInfo.numberOfNodesVisited += 1
        treeInfo.latestVisitedNodeValue = node.value
        reverseInOrderTraverse(node.left, k, treeInfo)

Complexity Analysis

• Time Complexity: $O(h+k)$ — in the worst case we will need to visit at most k nodes, but we also need to find the kth node and that node could potentially be further down our BST, thus the added h to account for the height of the tree
• Space Complexity: $O(h)$ — since this is a recursive algorithm we will have a call stack of length h.

---