Missing numbers

Date: 08-05-24

---

Problem

• We’re given an input array of length n where the values are unique and the range is supposed to be the length of array n + 2. This means that there will be two number in the range that will be missing from the list. Our function takes in this list and returns a new list with the two missing numbers, sorted numerically.

Example:

[1, 4, 3, 5] -> missing numbers [2, 6] ∴ return [2, 6]

---

Approach 1 (set):

• In this approach we can create a set that will contain our values in our input array. Then we will simply iterate over the values in the range of n + 2. For each n value we check if its in our set, which is a constant time operation, if it is not then we simply add it to our output array. If it is we keep going until we’ve finished iterating. What we’re left with is our final input array.

Implementation

# Set Solution | O(n) time | O(n) space
def missingNumbers(nums):
    # set
    includedNums = set(nums)
 
    # iterate over expected nums
    solution = []
    for num in range(1, len(nums) + 3):
        # if number not in set then add to solution
        if not num in includedNums:
            solution.append(num)
    return solution

Complexity Analysis

• Time Complexity: $O(n)$ — Iterating through the entire array length of n, checking the set is constant operation so we can disregard this time complexity.
• Space Complexity: $O(n)$ — the size of the set can be of length n

---

Approach 2 (using average):

• This solution requires a bit more arithmetic. To begin we will find the total sum of the values between 1...n+2, then we will find the total sum of the input array with the two missing values 1...n-2. Then we subtract these two totals, so sum1 - sum2. This will give us the difference between the two input arrays, with only the difference being the total of the two missing values. Using this we can find the average of this sum or the midpoint between these two numbers. This is done by dividing the numbers by two to find the average value in between the two missing numbers or essentially the midpoint. And since there are two values missing we can conclude that one number must be less than the average and one number must be greater than the average. Finally, to get to the solution we use the average to find the sum found to left of the average and the sum found to the right of that average. Then, we subtract expected sum minus the found sum for both halfs. this will give us the missing numbers.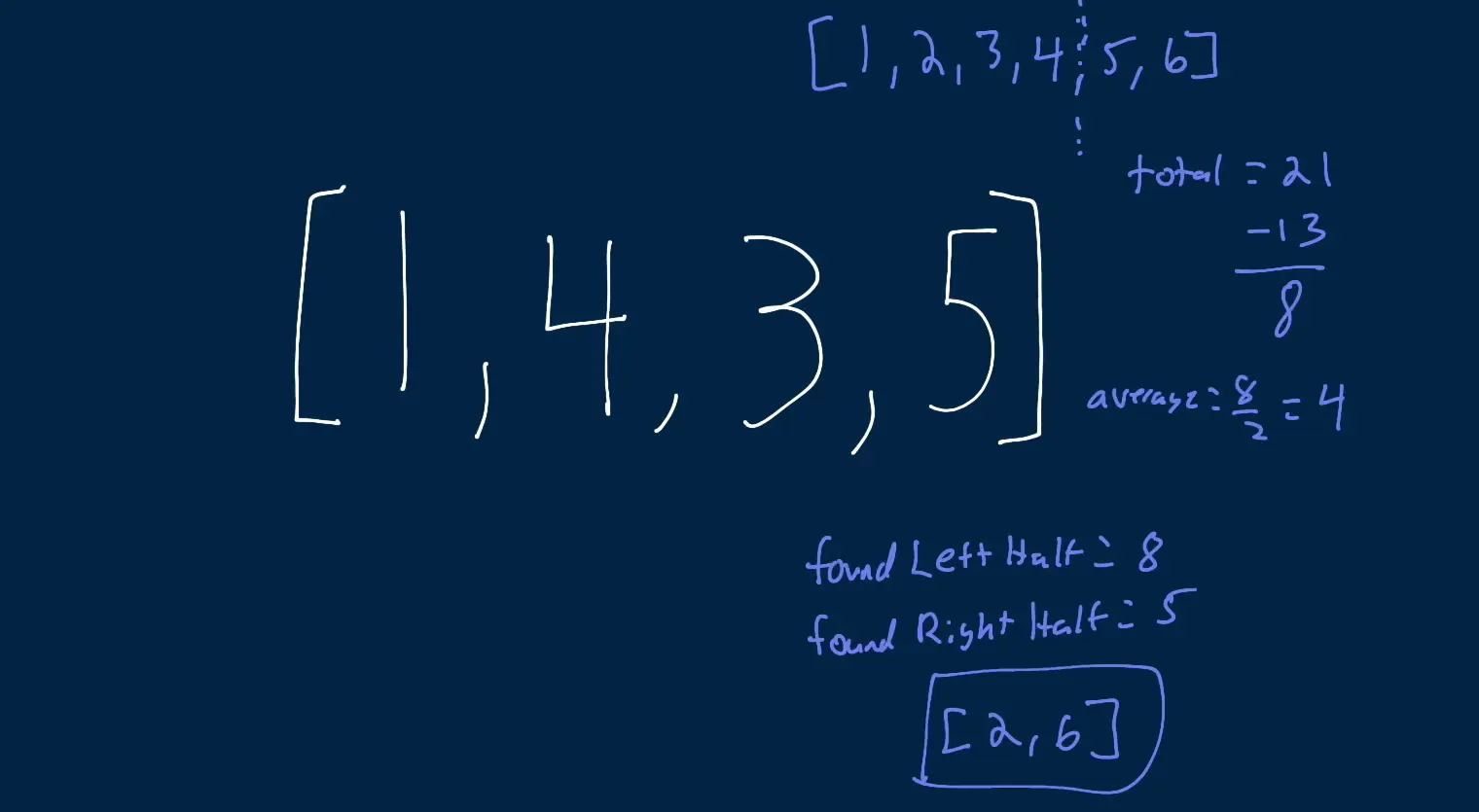
• 

Implementation

# Average Solution | O(n) time | O(1) space
def missingNumbers(nums):
    # total sum
    total = sum(range(1, len(nums) + 3))
 
    # find difference between expected and actual
    for num in nums:
        total -= num
 
    # find midpoint or average between the two values
    averageMissingValue = total // 2
 
    # Store value of left and right half
    foundFirstHalf = 0
    foundSecondHalf = 0
 
    # Calculate sum of left and right half of the average
    for num in nums:
        if num <= averageMissingValue:
            foundFirstHalf += num
        else:
            foundSecondHalf += num
 
    # Calculate the expected sum of the left and right half
    expectedFirstHalf = sum(range(1, averageMissingValue + 1))
    expectedSecondHalf = sum(range(averageMissingValue + 1, len(nums) + 3))
 
    # Find the difference to get the solution
    return [expectedFirstHalf - foundFirstHalf, expectedSecondHalf - foundSecondHalf]

Complexity Analysis

• Time Complexity: $O(n)$
• Space Complexity: $O(1)$

---

Approach 3 (Bitwise):

• The bitwise XOR solution to the missing numbers problem works by leveraging the properties of XOR where a number XORed with itself is 0, and a number XORed with 0 is the number itself. By XORing all the numbers from 0 to n and then XORing all the numbers in the array, all the numbers that appear in both sets cancel each other out. This cancellation leaves only the missing number, since it doesn’t get cancelled out by anything. This way, the final result of all these XOR operations is the missing number, efficiently found using O(n) time and O(1) space.
• XOR (exclusive OR) is a bitwise operation where the result is 1 if the bits being compared are different, and 0 if they are the same.
• XOR Solution Example

XOR Table

A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0
2	3	1
3	2	1
4	4	0
5	2	7

Implementation

# XOR Solution | O(n) time | O(1) space
def missingNumbers(nums):
    # Find XOR of two missing numbers
    # Do XOR of all expected values and all input values
    # Duplicates will cancel out
    solutionXOR = 0
 
    for i in range(0, len(nums) + 3):
        solutionXOR ^= i
 
        if i < len(nums):
            solutionXOR ^= nums[i]
 
 
    solution = [0,0]
 
    setBit = solutionXOR & -solutionXOR
 
    for i in range(0, len(nums) + 3):
        if i & setBit == 0:
            solution[0] ^= i
        else:
            solution[1] ^= i
 
        if i < len(nums):
            if nums[i] & setBit == 0:
                solution[0] ^= nums[i]
            else:
                solution[1] ^= nums[i]
 
    return sorted(solution)

Complexity Analysis

• Time Complexity:
• Space Complexity:

---

XOR Solution Example

Let’s work through an example to understand the XOR solution for finding missing numbers. We’ll also explain the XOR (^=) and AND (&) operations.

Setup

Suppose we have numbers from 1 to 7, and two numbers are missing. Our input array is:

nums = [1, 2, 4, 7]

The missing numbers are 3 and 5.

Step 1: XOR of all numbers

First, let’s explain the XOR operation:

• XOR (^) returns 1 if the bits are different, 0 if they’re the same.
• a ^= b is shorthand for a = a ^ b

Now, let’s calculate the XOR of all numbers from 0 to 7 and all numbers in our input array:

solutionXOR = 0
for i in range(0, 7):
    solutionXOR ^= i
    if i < len(nums):
        solutionXOR ^= nums[i]
 
# Step by step:
# 0 ^ 1 ^ 2 ^ 3 ^ 4 ^ 5 ^ 6 ^ 7 ^ 1 ^ 2 ^ 4 ^ 7
# = 3 ^ 5 (all other numbers cancel out)

After this step, solutionXOR = 3 ^ 5 = 6 (in binary: 110)

011  (3 in binary)
⊕ 101  (5 in binary)
-------
   110  (6 in binary)

Step 2: Finding the rightmost set bit

Now let’s explain the AND operation:

• AND (&) returns 1 if both bits are 1, otherwise 0.

To find the rightmost set bit:

setBit = solutionXOR & -solutionXOR
# 6 & -6 in binary:
#  0110
# &1010
# -----
#  0010

So, setBit = 2 (in binary: 010)

Rightmost Set Bit: Isolate the lowest bit where the missing numbers differ, helping to separate them into two distinct groups.

Step 3: Separating the numbers

Now we separate all numbers based on whether they have this bit set:

solution = [0, 0]
for i in range(0, 7):
    if i & setBit == 0:  # if the second bit is not set
        solution[0] ^= i
    else:  # if the second bit is set
        solution[1] ^= i
    if i < len(nums):
        if nums[i] & setBit == 0:
            solution[0] ^= nums[i]
        else:
            solution[1] ^= nums[i]
 
# Group 1 (second bit not set): 0, 1, 4, 5
# Group 2 (second bit set): 2, 3, 6, 7
 
# After XOR operations:
# solution[0] = 0 ^ 1 ^ 4 ^ 5 ^ 1 ^ 4 = 5
# solution[1] = 2 ^ 3 ^ 6 ^ 7 ^ 2 ^ 7 = 3

Separate and XOR: Group numbers based on this bit and XOR them within each group to cancel out all numbers except the missing ones.

Step 4: Return the result

return sorted([5, 3])  # Returns [3, 5]

And there we have our missing numbers!