Spiral Traverse

Date: 2024-07-27

Problem

• In this problem our objective is to take in a two dimensional array and traverse it in a spiral manner and return a one-dimensional array of all the array’s element in spiral order.
• This problem is popular in coding interview because it test how well a candidate can transcribe simple login into code.
• This problem can be solved recursively or iteratively.

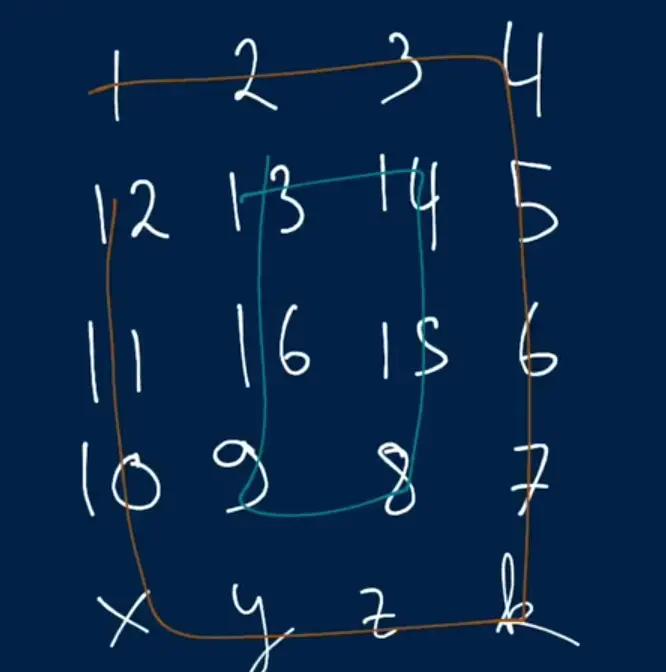
• We can essentially traverse through the outer perimeter of the 2d array and traverse through the inner perimeter.

Solution

• To solve this we can create some variables to indicate the sR (starting row) eR (ending row) and sC (starting column) and eC (ending column).
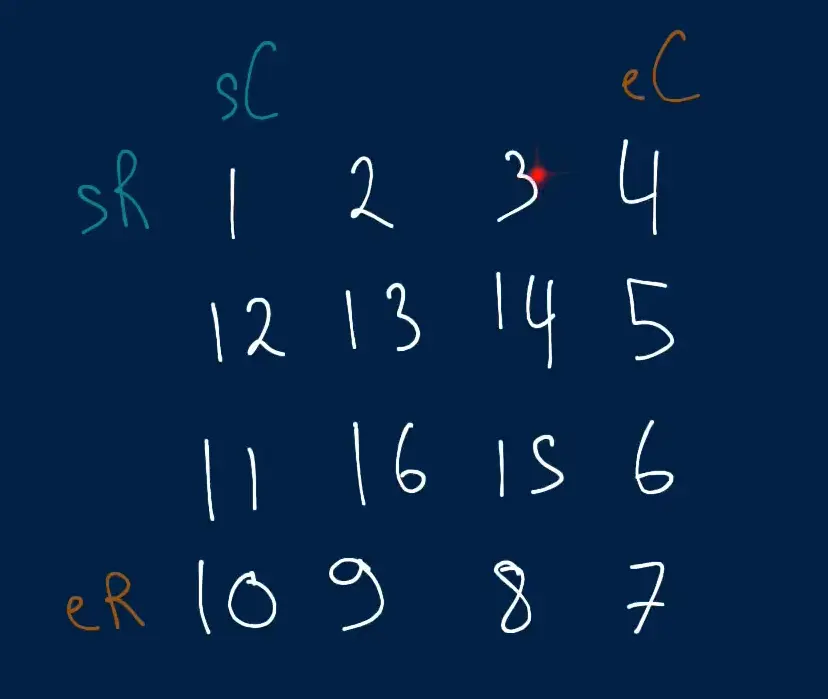
• We start at the starting row and begin traversing and adding to the final array. Starting off at 1 we can move on to the next value which is 2. moving the index as we go.
• Essentially in this solution we are using pointers and a starting and ending for columns and rows. Once we’ve iterated over the outer perimeter then we move the dimension inwards by one.
• Once sR has crossed eR and sC has crossed eC then we know that we don’t need to iterate anymore.
• Time Complexity: $O(N)$ , we are traversing the entire array. Space Complexity: $O(N)$ , since we are storing n values in a new array.

def spiralTraverse(array):
    # Declare result array
    result = []
 
    # Start row, end row, start col, end col
    startRow, endRow = 0, len(array) - 1
    startCol, endCol = 0, len(array[0]) - 1
 
    # <= and `and` is key for when one of the dimensions overlap, as well as the chance that you have
    # a one dimensional inner perimenter
    while startRow <= endRow and startCol <= endCol:
        for col in range(startCol, endCol + 1):
            result.append(array[startRow][col])
            
        for row in range(startRow + 1, endRow + 1):
            result.append(array[row][endCol])
            
        for col in reversed(range(startCol, endCol)):
            # This if statement is needed to account for the edge case
            # when there's a single row in the middle of a matrix. We don't
            # want to double count values in this row, which we've already counted
            # in the first for loop above. See test case 8.
            if startRow == endRow:
                break
            result.append(array[endRow][col])
            
        for row in reversed(range(startRow + 1, endRow)):
            # Edge case when there's a single column in the middle of the matrix.
            # In this case we don't want to double count the values in this column.
            # See test case 9
            if startCol == endCol:
                break
            result.append(array[row][startCol])
 
        # Shift the perimeter
        startRow += 1
        endRow -= 1
        startCol += 1
        endCol -= 1
            
    return result